Продолжаю решение задач на LeetCode. Сегодня буду решать задачу из категории Medium. Название задачи: Find First and Last Position of Element in Sorted Array.
Условие задачи
Дан отсортированный по возрастанию массив целых чисел. Необходимо найти первое и последнее вхождение заданного числа и вернуть соответствующие индексы. Если результат поиска не даст результата, следует вернуть [-1, -1].
При этом, необходимо написать алгоритм со сложностью выполнения O(log n).
Пример:
Input: nums = [5, 7, 7, 8, 8, 10] target = 8 Output: [3, 4]
Что такое сложность выполнения алгоритма
Прежде чем я перейду к решению, хочу, в первую очередь для себя, освежить знания о сложности алгоритмов. Это очень важный и сложный, по крайней мере для меня, вопрос. Однако понимание, как определяется сложность алгоритмов, какие критерии и метрики для этого используются, необходимо любому программисту, особенно тем, кто предполагает работу с большими объемами данных.
Время выполнения и используемый алгоритмом объем памяти – наиболее частые метрики оценки сложности выполнения алгоритма.
Что такое Big O
Big O используется для оценки верхней границы, наихудшего случая, временной сложности алгоритма. Big O показывает скорость роста времени исполнения алгоритма в зависимости от увеличения объема входных данных.
Варианты O-нотаций:
- O(1) – константная (постоянная) сложность;
- O(log n) – логарифмическая сложность;
- O(n) – линейная сложность;
- O(n log n) – линейная логарифмическая сложность.
Есть также еще квадратичная, кубическая, экспоненциальная и факториальная сложности. Информации об этом в интернете много, не хотелось бы дублировать.
O(log n)
Согласно условиям задачи, решение должно работать в пределах логарифмической сложности — O(log n).
Логарифмическая сложность характеризуется тем, что время выполнения растет медленно с увеличением объема входных данных. При этом, алгоритм с увеличением входных данных (N) замедляет свою работу, но не линейно, а в соответствии с логарифмической функцией.
Часто в качестве примера работы алгоритма со сложностью O(log n) приводится бинарный поиск в отсортированном списке. О, это же то, что мне нужно!
Бинарный поиск
Двоичный, он же бинарный, поиск (метод деления пополам, или дихотомия) – это один из классических алгоритмов. Условием возможности реализации бинарного поиска является отсортированные данные. Причем не имеет значения, по какому принципу они были отсортированы (по возрастанию или по убыванию).
Реализация бинарного поиска предполагает совершение следующего набора действий:
- определение центрального элемента массива;
- сравнение центрального элемента с искомым значением;
- в том случае, если искомое значение меньше центрального числа, то поиск продолжается в левой части (при условии, что массив отсортирован по возрастанию). Если искомое число больше, то поиск продолжаем в правой половине.
Такая последовательность действий осуществляется до тех пор, пока поиск не завершится либо успехом, либо поиск не даст результатов.
Существует два подхода в реализации бинарного поиска: итерационный и рекурсивный. В данной ситуации лучше подойдет итерационный подход, так как сложность реализации бинарного поиска рекурсией даст сложность выше требуемой по условию.
Итерационный подход
Для реализации данного подхода в решении поставленной задачи буду использовать цикл while. Для управления циклом объявляю переменную search_status с первоначальным значением True. Как только работа алгоритма закончится, переменной search_status будет присвоено значение False, и цикл будет завершен.
Но прежде чем начнет работу цикл while, нужно проверить, а есть ли в полученном списке целых чисел искомое число. Ведь если его нет, то вся дальнейшая работа будет бессмысленна. В такой ситуации по условиям задачи необходимо вернуть список [-1, -1].
if target not in nums:
return [-1, -1]
Если условие пройдено, то можно переходить и к описанию цикла. Хотя…
Нет, надо еще определить несколько переменных, чтобы цикл начал свою работу. Нужно определить длину списка nums, а также стартовый и последний индексы элементов в списке, которые будут определять диапазон поиска.
length_nums = len(nums) start_index = 0 end_index = length_nums - 1
На этом моменте я хорошенько призадумался. Первая мысль, которую я попробовал реализовать, это сразу, до работы цикла, рассчитать индекс среднего элемента в списке, который является отправной точкой при работе с алгоритмом бинарного поиска.
Но особых результатов это не принесло, а потом и вовсе пришлось переключиться на другие задачи, юридического свойства, работу пока эту еще я себе не отменил.
Прошел день, и я решил подобраться к решению данной задачи немного по-другому, как говорили на учебе в Яндекс Практикуме, слона надо есть по частям. Вот и я решил разделить эту задачу на две подзадачи:
- первая подзадача — найти в списке искомое число и получить его индекс;
- вторая подзадача – определить первое и последнее вхождение этого числа в список.
Получение индекса искомого числа
Итак, первая подзадача решена, получаю индекс элемента, который равен искомому. За эту процедуру отвечает цикл while:
# переменная, которая отвечает за управление работой цикла
search_status = True
while search_status:
# вычисление индекса среднего элемента в искомой области списка
middle_index = (start_index + end_index) // 2
# Проверка на совпадение среднего элемента искомой области списка
# с искомым элементом
if target == nums[middle_index]:
# если совпадение найдено, флаг search_status получает
# значение False, и работа цикла завершается
search_status = False
# Если условие выше не выполнено, то определяем, в какой
# части списка нужно искать. если искомое число меньше
# среднего элемента, то берем левую часть списка
if target < nums[middle_index]:
start_index = 0
end_index = middle_index
# Если искомое число больше, то берем правый отрезок списка
if target > nums[middle_index]:
start_index = middle_index + 1
end_index = length_nums
Определение индекса первого и последнего вхождения
Перехожу к решению второй подзадачи. У меня есть индекс элемента, который равен искомому. Но этого для решения задачи недостаточно.
На всякий случай, для себя, напомню, что мне нужно вернуть индекс первого и последнего вхождения искомого числа. Список отсортированный, поэтому надо просто поочередно сравнивать элементы в списке. Вопрос, в какую сторону двигаться. Или сразу в обе?
Вариант в обе выглядит интересным, попробую его реализовать на практике. Для этого мне понадобиться цикл for, точнее два цикла for. Один будет сравнивать элементы списка с заданным числом вправо, а другой пойдет влево. Сравнение будет происходить на неравенство. Как только элемент списка перестает быть равным искомому, цикл for прерывается с помощью инструкции break.
Тут я вижу два случая, которые следует, по крайней мере на данный момент, обработать отдельно. Дело в том, что полученный в результате бинарного поиска индекс искомого элемента может быть как последним в списке, так и первым.
Порассуждаю. Если индекс найденного элемента равен 0, то есть этот элемент первый в списке, то этот индекс и будет индексом первого вхождения. Осталось, двигаясь вправо по списку, найти последний элемент, который равен искомому, и определить его индекс. Это будет индекс последнего вхождения в список.
В свою очередь, если индекс найденного элемента равен последнему индексу в списке, то двигаться вправо не имеет смысла, да и мы обязательно получим ошибку. А найденный индекс будет индексом последнего вхождения. Осталось найти стартовый индекс, для чего нужно двигаться влево по списку.
Итак, делаю первую проверку на то, является ли найденный индекс первым элементом в списке:
if middle_index == 0:
# определяю индекс первого вхождения элемента в список
start_position = 0
Если условие выполнено, то есть первый элемент списка с индексом 0 равен искомому, то индекс первого вхождение будет равен 0. Теперь надо двигаться вправо с помощью цикла for. Перебирать буду индексы от 1 (второго элемента в списке) и до последнего элемента в списке (список может состоять полностью из равнозначных элементов). Как только встретим элемент, который окажется не равным искомому, цикл останавливаем и определяем индекс последнего вхождения. Говоря на языке Python, это будет звучать так:
if middle_index == 0:
start_position = 0
for index in range(middle_index + 1, length_nums):
if nums[index] != target:
# Потому что на предыдущей итерации цикла это условие не сработало,
# а это значит, что nums[index] = target. Следовательно, индекс
# последнего вхождения равен индексу на предыдущей итерации, то есть index - 1
end_position = index - 1
break
return [start_position, end_position]
Теперь можно описать и вторую ситуацию, когда совпадающий элемент списка является последним элементом.
Также используя цикл for прохожусь по элементам списка от предпоследнего до первого, то есть в обратном порядке. Тут чего-то принципиально отличающегося от предыдущего участка кода нет, поэтому код без комментариев.
if middle_index == length_nums - 1:
end_position = length_nums - 1
for index in range(middle_index - 1, -1, -1):
if nums[index] != target:
start_position = index + 1
break
return [start_position, end_position]
Теперь надо описать все остальные случаи. Возможно, сейчас код будет дублироваться, но для первого подхода это норм, потом можно будет подумать, как оптимизировать код, но это после того, как LeetCode даст мне зеленый свет. Пока я вижу только красный.
Рассуждение. Допустим, индекс совпадающего элемента равен 4, а длина всего списка равна 6. Я не знаю, что находится слева и справа от найденного элемента. Следовательно, мне надо посмотреть и там, и там.
Вот что я точно знаю, что индекс первого вхождения заданного числа находится слева, либо равен индексу искомого числа, а индекс последнего элемента находится справа, либо также равен индексу искомого числа. Согласитесь, что искомое числе в списке может встретится только один раз, и это надо учитывать.
Таким образом, мне нужно два цикла for: один для поиска индекса первого вхождения, второй для поиска последнего вхождения. Один цикл движется влево, второй – вправо.
Вот такой код у меня получился:
for index in range(middle_index - 1, -1, -1):
if nums[index] != target:
start_position = index + 1
break
for index in range(middle_index + 1, length_nums):
if nums[index] != target:
end_position = index - 1
break
return [start_position, end_position]
Вот только есть проблемка: если на вход метод получает список {1, 2, 2}, а в качестве искомого числа число 2, то сразу получаю следующую ошибку:
UnboundLocalError: cannot access local variable ‘end_position’ where it is not associated with a value
Проблема заключается в том, что приведенный выше код не может определить индекс последнего вхождения. Индекс первого вхождения определен верно. Надо разбираться.
Еще раз взглянув на список {1, 2, 2}, я понял, что у меня условие не срабатывает, так как при работе цикла, который отвечает за поиск индекса последнего вхождения, просто не находится элемента, который не равен искомому.
Цикл не обнаружил элемент, который не равен искомому. Следовательно, надо такое поведение описать. Действительно, все последующие элементы до конца списка могут быть равными искомому. Следовательно, последним индексом вхождения будет индекс последнего элемента. Первое, что приходит на ум, добавить инструкцию else.
Аналогичная проблема возникает и со стартовым индексом, так как там также не предусмотрен случай, что все элементы в начале списка могут быть одинаковыми. Добавлю и туда инструкцию else.
В итоге, новая редакция этого участка кода будет выглядеть вот так:
for index in range(middle_index - 1, -1, -1):
if nums[index] != target:
start_position = index + 1
break
else:
start_position = 0
for index in range(middle_index + 1, length_nums):
if nums[index] != target:
end_position = index - 1
break
else:
end_position = length_nums - 1
return [start_position, end_position]
И тут, проверяя работу кода на платформе LeetCode, я получил неожиданный для себя результат. А именно предупреждение: time limit exceeded. Тут не надо быть гением, чтобы понять, в какой части кода закралась ошибка. Безусловно, речь идет о цикле while, который уходит в бесконечность из-за неверного описания.
Так и есть — проблема была в том, что я неправильно определял границы поискового диапазона в списке. Я все время в качестве индекса стартового элемента указывал 0, а в качестве индекса, который отсекает границу в списке, – индекс последнего элемента всего списка. Но это же не так. Дело в том, что границы поискового диапазона не статичны, они меняются на каждой итерации цикла в зависимости от заданных условий.
Поправив цикл while, вновь пошел тестировать свой код.
Результат: получен зеленый свет!
Да, мой код рабочий, и все тесты для данной задачи на LeetCode пройдены.
- Runtime – 55 ms — обгоняет 76,97% пользователей Python
- Memory – 12,79 mb — обгоняет 82,90 % пользователей Python
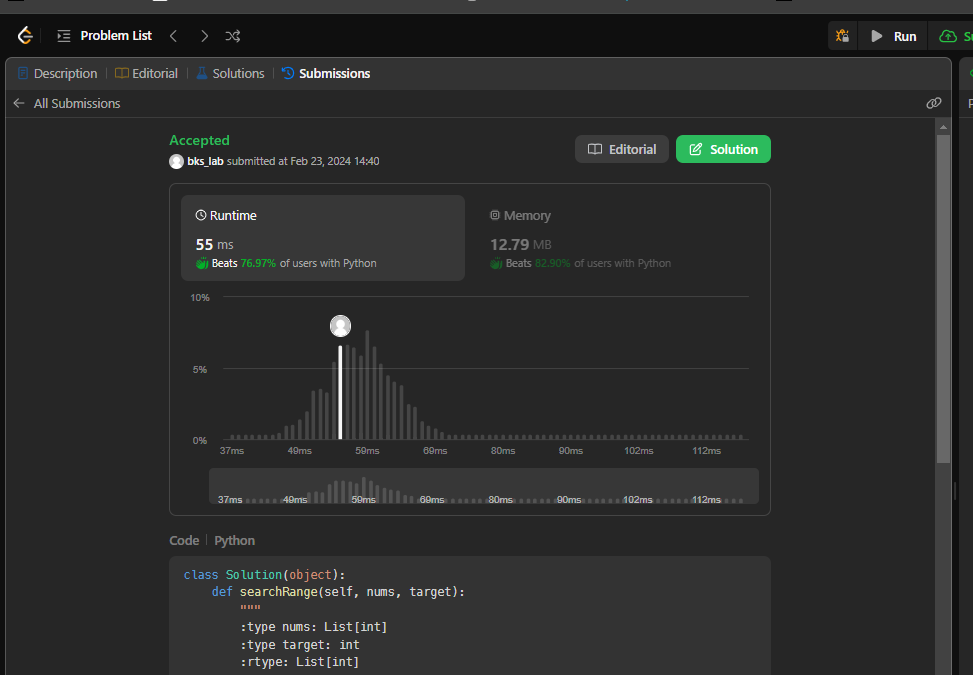
Полный код решенной задачи:
class Solution(object):
def searchRange(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
if target not in nums:
return [-1, -1]
length_nums = len(nums)
start_index = 0
end_index = length_nums - 1
if all(el == nums[0] for el in nums):
return [start_index, end_index]
search_status = True
while search_status:
middle_index = (start_index + end_index) // 2
if target == nums[middle_index]:
search_status = False
if target < nums[middle_index]:
start_index = start_index
end_index = middle_index
if target > nums[middle_index]:
start_index = middle_index + 1
end_index = end_index
if middle_index == 0:
start_position = 0
for index in range(middle_index + 1, length_nums):
if nums[index] != target:
end_position = index - 1
break
return [start_position, end_position]
if middle_index == length_nums - 1:
end_position = length_nums - 1
for index in range(middle_index - 1, -1, -1):
if nums[index] != target:
start_position = index + 1
break
return [start_position, end_position]
for index in range(middle_index - 1, -1, -1):
if nums[index] != target:
start_position = index + 1
break
else:
start_position = 0
for index in range(middle_index + 1, length_nums):
if nums[index] != target:
end_position = index - 1
break
else:
end_position = length_nums - 1
return [start_position, end_position]
Я доволен результатом и могу двигаться дальше. Ну, а дальше подготовка публикации по работе над Telegram ботом. В частности, поговорим про Docker, PostgreSQL, Redis и как все это собрать в одно с самим ботом. Все публикации про бот смотрите в рубрике Telegram bot.
Публикации, где я делюсь своими рассуждениями в ходе решения задач, собраны в рубрике Решаем задачи.
Если есть вопросы, критические замечания или предложения, пишите мне в Telegram, в Вконтакте или на почту bks2408@mail.ru